Overview
Distinct
배열 내 원소 중 Unique한 것의 수를 구하라
Solution
주어진 벡터를 이용하여 std::set 을 만든다
Set은 정렬되어 있으며 중복을 허용하지 않는 특성이 있다.
#include <set>
int solution(vector<int> &A)
{
std::set<int> unique(A.begin(), A.end());
return unique.size();
}
MaxProductOfThree
배열에서 임의의 세 원소를 곱하여 가장 큰 값을 만들어라
Solution
정렬 후 가장 큰 세 원소를 이용한다. 단, 원소는 음수가 가능하기 때문에 가장 작은(절대값이 가장 큰) 두 원소의 곱을 고려해야한다.
세 개를 곱하면 다시 음수가 되기 때문에 고려하지 않는다.
#include <algorithm>
#include <cmath>
int solution(vector<int> &A)
{
std::sort(A.begin(), A.end());
return std::max(A[0] * A[1] * A[A.size() - 1], A[A.size() - 1] * A[A.size() - 2] * A[A.size() - 3]);
}
Triangle
주어진 길이의 모서리들로 삼각형을 만들 수 있는 지 판단하라
Solution
세 모서리 A, B, C의 길이가 A <= B <= C 일 때, C < A + B 를 만족해야 삼각형을 만들 수 있다.
따라서, 모서리의 길이를 정렬한 후 인접한 세 모서리가 C < A + B를 만족하는 지 확인한다.
인접한(i, i + 1, i + 2) 원소들로 만족하지 않는다면 다른 인접하지 않은 원소들(ex) i, i + 1, i + 3)으로도 만족하지 않기 때문에 한 원소당 1번의 검사로 충분하다 (O(N))
#include <algorithm>
int solution(vector<int> &A)
{
// A의 크기는 3 미만일 수 있음
if(A.size() < 3)
return 0;
// A의 원소는 int_max 까지 가능하므로 둘을 더한 값은 int보다 큰 자료형이어야 함
unsigned long long tmp;
std::sort(A.begin(), A.end());
for(auto i = 0 ; i < A.size() - 2 ; ++i)
{
tmp = A[i] + A[i + 1];
if( tmp > static_cast<unsigned long long>(A[i + 2]))
return 1;
}
return 0;
}
NumberOfDiscIntersections
개인적으로 가장 힘들었던 문제들 중 하나. 솔루션 여러 개를 뒤지고 십 수번 그려낸 뒤에야 이해했다 :(
평면 상의 디스크들의 접점의 수를 구하라
Failure
가장 단순하게 각 디스크의 Left/Right가 다른 디스크의 Left, Right 사이에 포함되는 지 비교했다. 당연하게도 O(N^2)의 복잡도로는 O(N * lg(N))의 성능 테스트를 통과할 수 없었다.
Solution
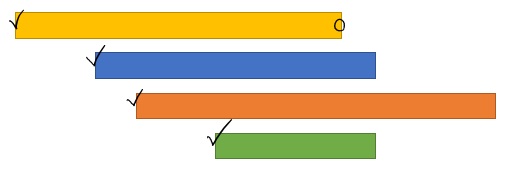
Left와 Right가 각각 정렬되어 있을 때, 가장 작은 Right(O 마크)보다 작은 Left(V 마크)들은 반드시 가장 작은 Right(O 마크)보다 큰 Right를 갖는다. 즉, 접점을 갖는다.
O 마크의 Right가 가장 작으니까 당연히 나머지 Right들은 그보다 크다.
이 작업을 각 Right마다 새로 하는 것이 아니라 Accumulate하게 진행한다.
- R > L 인 L의 수(current)를 구한다.
- –current;
- current는 반드시 자기 자신을 포함한다.
- 또한 다음 R에서 겹치지 않을 수 있는 경우의 수를 제거한다.
- current는 초기화하지 않고 계속해서 사용한다.
#include <vector>
#include <algorithm>
int solution(vector<int> &A)
{
unsigned int N = A.size();
std::vector<long long>left(N), right(N);
// 계산되는 값들의 타입을 맞춰주도록 한다
for (unsigned long long i = 0; i < N; ++i)
{
left[i] = i - A[i];
right[i] = i + A[i];
}
std::sort(left.begin(), left.end());
std::sort(right.begin(), right.end());
long long result{}, current{};
unsigned long long lIndex{}, rIndex{};
for (auto i = 0; i < N; ++i)
{
while (lIndex < N && left[lIndex] <= right[rIndex])
{
++current;
++lIndex;
}
--current;
result += current;
++rIndex;
std::cout << current << " ";
if (result > 10000000)
return -1;
}
return result;
}
